Imagine this scenario
You receive an excessively hot cup of coffee at your local coffee shop. As it’s the first cup of the day, your main objective is to consume the caffeine as quickly as possible. Unfortunately, if you were to gulp down the coffee the barista just handed you now, you would most certainly end up taking a trip to the hospital for second-degree burns.
Fortunately you have at your disposal a caraffe of properly chilled cream and a dreamy appreciation for dynamic systems. The question is: to reach your ideal coffee-consumption temperature as quickly as possible, should you mix the cream immediately into the coffee or should you wait a certain amount of time?
Assuming you have (groggily) estimated the following variables:
| Variable | Meaning |
|---|---|
| \(T_{Cof}\) | Temperature of the coffee |
| \(T_{D}\) | Desired temperature for the coffee |
| \(T_{R}\) | Temperature of the room |
| \(T_{Cr}\) | Temperature of the cream |
| \(k\) | Cooling rate coefficient |
| \(r\) | Percentage of coffee in final mixture |
You can use Newton’s law of cooling to get started:
\[\dot{T}(t) = -k (T(t) - T_R)\]
This tells you that the change in surface temperature of an object is proportional to difference between the object’s temperature and the surrounding environment.
From this you know that the temperature of the coffee at time \(t\) is given by the following solution to the above differential equation:
\[T(t) = T_R + \left(T_0 - T_R \right)e^{-kt}\]
Where \(T_0\) represents the initial temperature of an object and \(T_R\) the temperature of the surrounding environment.
Two strategies come to mind: immediately add the cream to the coffee, or wait until adding the cream will reduce the temperature just enough to achieve the desired temperature. But which will bring you your caffeine fix fastest?
We’ll make the simplifying assumption that the mixing process is instantaneous and that the temperature of the final mixture is a weighted average of the temperatures of the two liquids, relative to their volume. We’ll further simplify this step by expressing our result in terms of the percentage of coffee in the final mixture, \(r\).
Interactive R Shiny App
I made an interactive plot where you can dynamically alter (play with) the problem parameters using RStudio’s Shiny App. If you have R 3.x and Shiny installed, you can run the app by simply calling runGist(9370271) after loading Shiny. The app is available as a Github gist here.
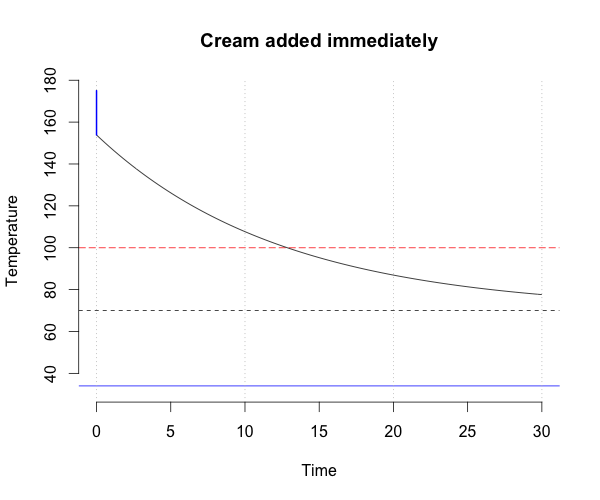
Mix immediately
If the cream is added immediately, then the effective initial temperature of the coffee is \(rT_{Cof}+(1-r)T_{Cr}\) and this mixture will reach the desired temperature in time \(\tau_1\) units:
\[T_D = T_R + \left(rT_{Cof}+(1-r)T_{Cr} - T_R \right)e^{-k\tau_1}\]
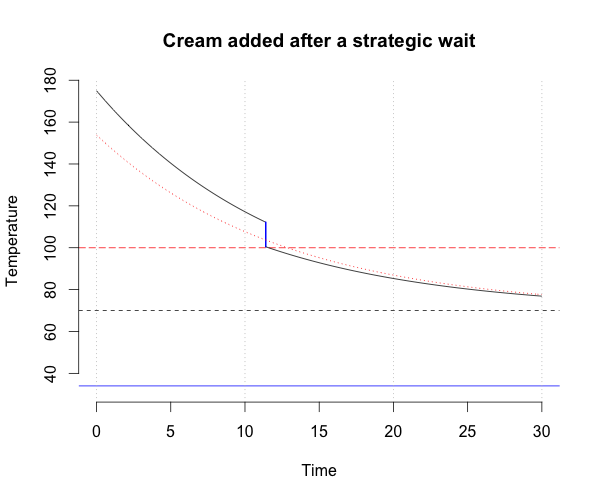
Wait the right amount of time
If instead the cream is added at just the right time so that, when the coffee is combined with the cream, the resultant mixture will have the desired temperature, then the time at which the cream should be added (and also the time at which \(T_D\) is achieved) is \(\tau_2\), given as follows:
\[T_D = \left[ T_R + \left( T_{Cof} - T_R \right) e^{-k\tau_2} \right] r + (1-r)T_{Cr}\]
Comparing \(\tau_1\) and \(\tau_2\)
The right hand side of the above equations are equivalent, so the question becomes which is smaller, \(\tau_1\) or \(\tau_2\)? Solving for the waiting time of each yields the following equations:
\[\begin{aligned} \tau_1 &= - \frac 1 k \ln \left[ \frac{T_D - T_R}{rT_{Cof} +(1-r)T_{Cr} - T_R} \right] \\\ & \\\ \tau_2 &= -\frac 1 k \ln \left[ \frac{T_D - (1-r)T_{Cr} - rT_R}{rT_{Cof} - rT_R} \right]\\\ \end{aligned}\]
Because the question is which waiting time is shorter and \(\ln(x) \to - \infty\) as \(x \to 0\), the question then becomes which fraction inside the \(\ln\) functions is smaller. In this, we will assume that, given the physical characteristics of the problem, \(T_{Cr} < T_R < T_D < T_{Cof}\), and that \(0 \leq r \leq 1\).
To give away the punchline a little, what we’ll find is that by using the simple assumptions above we can show that the numerator in the \(\tau_1\) expression is smaller than the numerator in the \(\tau_2\) expression, and that the denominator in \(\tau_1\) is bigger than the denominator in \(\tau_2\). If this is true, then clearly \(\tau_1 > \tau_2\) as \(- \ln \left( \frac{-}{+} \right) < - \ln \left( \frac{+}{-} \right)\).
Let’s first consider the numerators. \(T_D\) is the same in both, so we need to compare the amount subtracted from it: \(T_R\) vs \((1-r)T_{Cr} + rT_rR\).
Notice that because \(T_{Cr} < T_R\) \[T_R = (1-r)T_R + rT_R > (1-r)T_{Cr} + rT_R\] and thus \(T_D - T_R < T_D - (1-r)T_{Cr} - rT_R\), indicating that the numerator in the expression for \(\tau_1\) is less than that of the expression for \(\tau_2\).
Second, consider the denominators, specifically the amount subtracted from \(rT_{Cof}\) in both: \(T_R - (1-r)T_{Cr}\) vs \(rT_R\).
Here notice that \(rT_R = T_R - (1-r)T_R\). Then, from \(T_{Cr} < T_R\) we can conclude that \((1-r)T_{Cr} < (1-r)T_R\), which further implies that \(T_R - (1-r)T_{Cr} > T_R - (1-r) T_R = rT_R\). Thus the denominator in the expression for \(\tau_1\) is greater than the denominator in the expression of \(\tau_2\).
\[\begin{aligned} T_D - T_R &< T_D - (1-r)T_{Cr} - rT_R \\\ & \\\ rT_{Cof} +(1-r)T_{Cr} - T_R &> rT_{Cof} - rT_R \\\ \end{aligned}\]
From this we can finally conclude that the fraction in the expression for \(\tau_1\) has a smaller numerator and larger denominator than that of \(\tau_2\). The interpretation of this result is that waiting until \(\tau_2\) to allows the coffee to reach the desired temperature faster than adding the cream immediately. The reduction in waiting time is a function of initial conditions and depends on the temperature differential, in particular between the cream and the room and coffee.
So, if you need faster caffeine intake: wait a bit before adding your cold cream (or almond milk). On the flip side, if you want to keep your coffee hotter for longer, add your cream right away. Or get a real coffee habit and skip the cream entirely1.
Footnotes
I can’t believe I made it through this whole explanation without mentioning almond milk. I’m lactose intolerant. Almond milk is great. But coffee is best black. Not black as in “no cream”. Black as in “dark matter” or “black hole”.↩︎